Zerstreuungskreise bei verschiedenen Filmformaten (2007)
Fragestellung: Kleinbild oder Mittelformat für Portraits?
Meine Ausgangsfrage: wie verhält es sich mit der Schärfentiefe bei den verschiedenen Filmformaten?
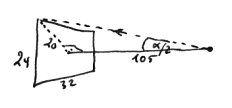
Ich untersuche also die Grösse des Zerstreuungskreises in Abhängigkeit von der Formatdiagonalen , der Brennweite , der Blendenzahl und der fokussierten Entfernung .
Dazu etwas Linsenphysik:
Es gilt also die Linsengleichung (1):
Und für die Öffnung gilt (2):
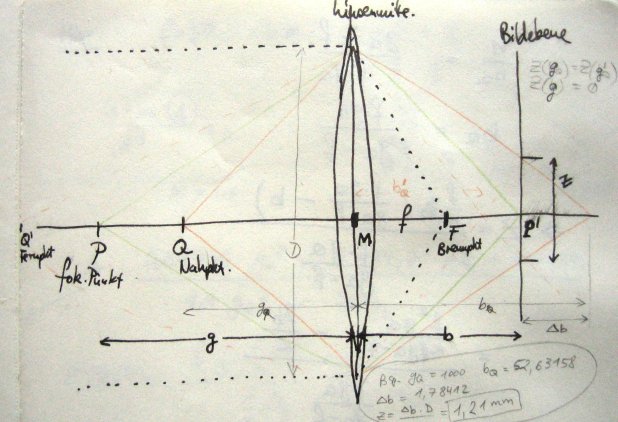
gesucht ist :
(s. Grafik)
(Strahlensatz)
Nach (1) gilt fuer :
(Analog für .) Also komplett:
Januar 2008
Bzw. einfacher:
Erste Eindrücke von Z
Wir haben jetzt einen Ausdruck für in Abhängigkeit von , jetzt genannt. Wir nehmen zum Plotten den Absolutwert, um nur positive Durchmesser zu erhalten.
Z(f,g,K,x)= abs((f/K) * ((f*x/(x-f))-(f*g/(g-f))) / (f*x/(x-f)))
Z(f,g,K,x)= abs((1/K) * ((f*x/(x-f))-(f*g/(g-f))) / (x/(x-f)))
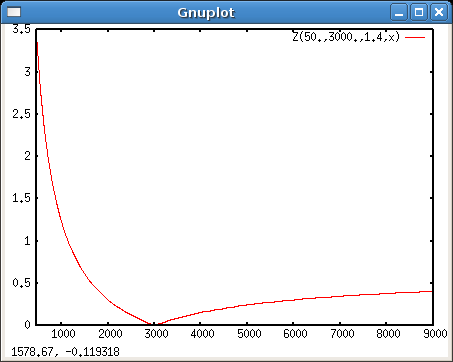
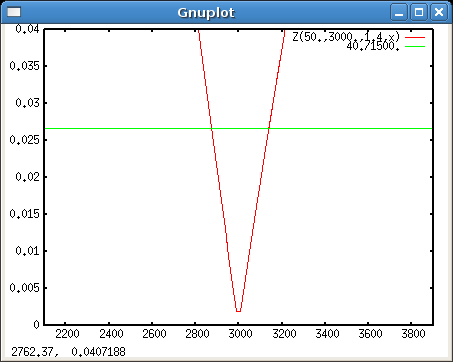
Lassen wir uns doch mal ein paar Kurven zeigen! Nehmen wir als Beispiel ein Normalobjektiv f=50 mm bei Blende K=1.4 und fokussierter Entfernung g=3000 mm:
set samples 500 # WICHTIG! plot [450:9000] Z(50.,3000.,1.4,x)
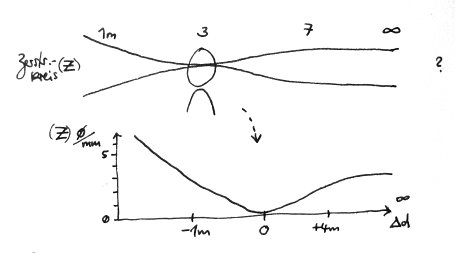
Die etwas eigentümliche Zu- und Abnahme der Zerstreuungskreis-Durchmesser ist hier zu erkennen. Gegenstände, die immer näher an der Linse liegen, werden immer schneller immer unschärfer. Entfernte Gegenstände werden auch unschärfer, die Unschärfe hat aber als Grenzwert (für ):
Hier also 0.605 mm.
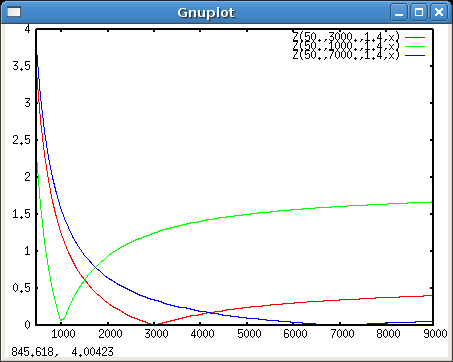
Was passiert, wenn wir das Objektiv auf verschiedene Entfernungen fokussieren? Als Beispiele g=1000, 3000, 7000 mm:
plot [450:9000] Z(50.,1000.,1.4,x), Z(50.,3000.,1.4,x), Z(50.,7000.,1.4,x)
Man sieht, dass sich ausser dem Punkt der maximalen Schärfe, der natürlich bei der fokussierten Entfernung liegt, hauptsächlich der Fern-Zerstreuungskreis ändert, er wird grösser mit kleinerem .
Die Kurven für ferne Fokussierung laufen auch flacher, was eine grössere Schärfentiefe bedeutet! Ich zeige den Standardwert für scharfe Abbildung, . (Dahinter steckt die Regel, dass 1/1500 der Formatdiagonale die maximale Auflösung des Auges sein sollen.) Für Fokussierung auf 3000 mm:
set yrange [0:0.04] d=40; plot Z(50.,3000.,1.4,x), d/1500.
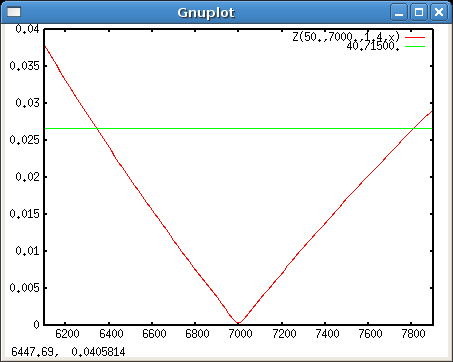
Für Fokussierung auf 7000 mm:
d=40; plot Z(50.,7000.,1.4,x), d/1500.
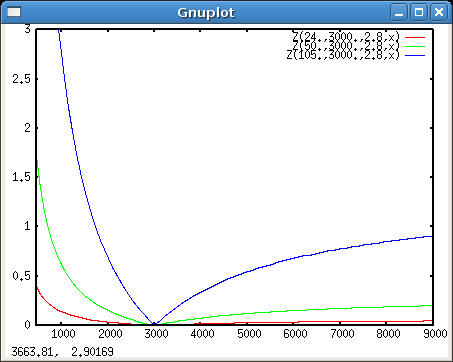
Jetzt könnten noch verschiedene Brennweiten interessieren:
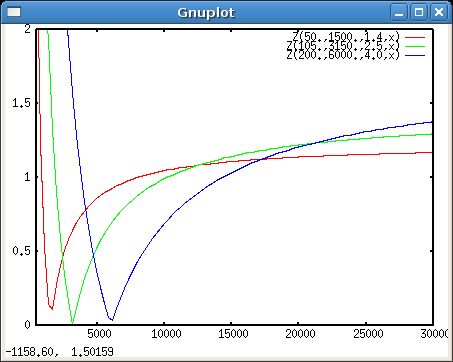
reset y plot Z(24.,3000.,2.8,x), Z(50.,3000.,2.8,x), Z(105.,3000.,2.8,x)
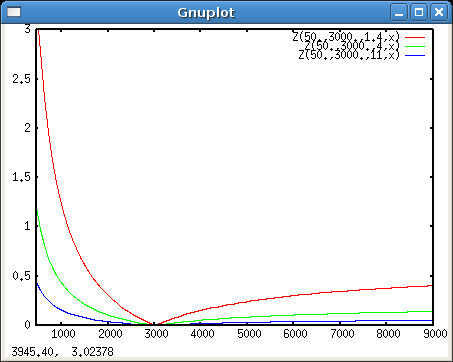
Sowie verschiedene Blenden:
plot Z(50.,3000.,1.4,x), Z(50.,3000.,4.,x), Z(50.,3000.,11.,x)
Kleinbild, Mittelformat...
Jetzt zu den verschiedenen Filmformaten. Um die Objektive zu vergleichen, müssen wir ihre Bildwinkel kennen. Ich betrachte die Formatdiagonale von 6x6, , sowie Kleinbild, nutzbares Bild 24x32, . (Kleinbild auf Seitenverhältnis 4:3 beschnitten.)
Der Bildwinkel lässt sich so berechnen:
Kleine Tabelle für Kleinbild- und 6x6-Objektive:
a(f,d)=2*(atan(d/(2.*f))/2/pi*360)
| (KB) | (6x6) | ||
|---|---|---|---|
| 17 | 99.27° | ||
| 20 | 90.00° | 40 | 89.42° |
| 24 | 79.61° | 50 | 76.76° |
| 28 | 71.08° | ||
| 60 | 66.85° | ||
| 35 | 59.49° | ||
| 80 | 52.67° | ||
| 50 | 43.60° | 100 | 43.21° |
| 60 | 36.87° | 120 | 36.53° |
| 135 | 32.70° | ||
| 150 | 29.58° | ||
| 85 | 26.48° | 180 | 24.81° |
| 105 | 21.57° | ||
| 250 | 18.00° | ||
| 135 | 16.85° | ||
| 150 | 15.19° | ||
| 180 | 12.68° | 350 | 12.91° |
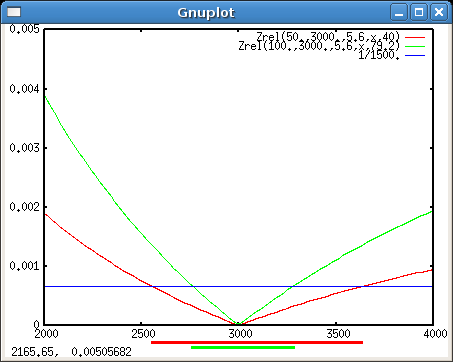
Ich definiere jetzt ein als , damit können wir Zerstreuungskreis-Durchmesser auf Endprints der gleichen Grösse vergleichen.
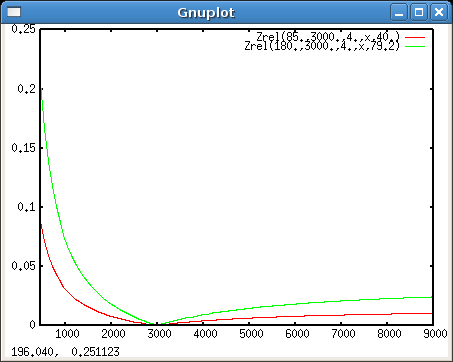
Zrel(f,g,K,x,d)=Z(f,g,K,x)/d plot [450:9000] Zrel(85.,3000.,4.,x,40.), Zrel(180.,3000.,4.,x,79.2)
Zwei Objektive gleichen Bildwinkels (85 mm und 180 mm) auf dem jeweiligen Format. Das 180er zeichnet mehr als relativ doppelt so grosse Zerstreuungskreise, bei 450 mm z.B. 8.8 % vs. 20.6 % der Formatdiagonalen!
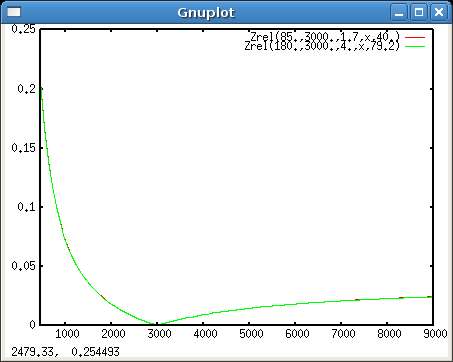
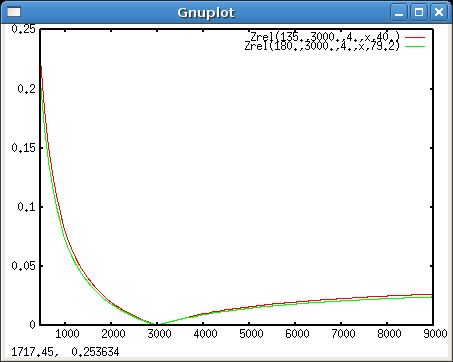
Wir brauchen Blende 1.7 beim 85er, um die gleiche Unschärfe im Print zu erhalten, wie beim 180er auf Blende 4 - oder ein 135er bei Blende 4:
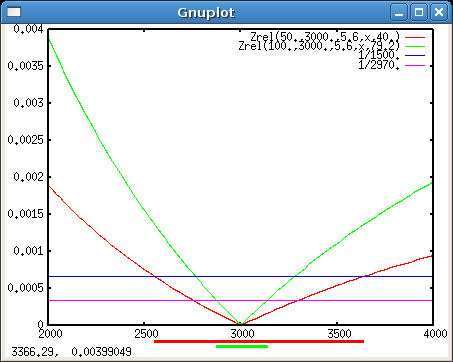
Die relative Grenze für Schärfe als , ergibt sich dies:
Wenn man beide Formate um den gleichen Faktor vergrössert (d.h. 6x6 liefert grössere Prints), muss die Grenze absolut gleich sein, die Schärfentiefe bei 6x6 ist also noch viel geringer:
Allgemeines über Z
Ich wandle mal die Gleichung um:
proportional zu , proportional zu ,
proportional zu .
Welches Portraittele hat die grösste Zerstreuung?
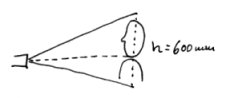
Aufgabe ist die Abbildung eines Schulterportraits, Diagonale des Objektfelds ist 600 mm.
| /mm | /° | /mm | , =2.8 |
|---|
| 1500 | 43.60 | 50 | 0.616 | @1.4: 1.232 |
| 2550 | 26.48 | 85 | 1.047 | |
| 3150 | 21.57 | 105 | 1.293 | @2.5: 1.448 |
| 4051 | 16.85 | 135 | 1.661 | |
| 4500 | 15.19 | 150 | 1.847 | |
| 6000 | 11.42 | 200 | 2.463 | @4.0: 1.724 |
also bei :
proportional zu , proportional zu !!
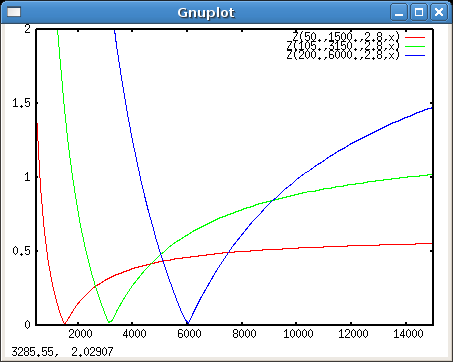
D.h. für das gleiche Schulterportrait liefert ein 105er ca. doppelte Zerstreuung eines 50ers (bei gleicher Blende):
Wenn man grössere Blenden bei kürzeren Brennweiten ausnutzt (50/1.4 etc.), ergibt sich immer noch ein Vorteil für die lange Brennweite, allerdings wirklich nur noch für extrem weit entfernte Hintergründe:
D.h. für Trennung naher Hintergründe vom Objekt ist hier ein Vorteil bei der kurzen Brennweite mit Offenblende!
Januar 2008
Portraittele, Teil 2
Die Frage jetzt etwas präzisiert: Ich will auf ein Objektfeld von 600 mm Höhe scharf stellen, wie oben; also ein Schulterportrait. Schärfe liegt auf den Augen des Portraitierten.
Jetzt möchte ich aber seinen Hinterkopf möglichst unscharf haben, d.h. eine möglichst dünne Schärfe-Ebene. Ich vergleiche deshalb verschiedene Objektive und Filmformate auf die Zersteuung 200 mm hinter der Schärfe-Ebene.
wie oben:
KB:
| /mm | /° | /mm | (+200 mm) | (+200 mm)/% | |
|---|---|---|---|---|---|
| 1500 | 43.60 | 50 | 1.4 | 0.14489 | 0.3622 % |
| 2550 | 26.48 | 85 | 2.0 | 0.10658 | 0.2665 % |
| 3150 | 21.57 | 105 | 2.5 | 0.08646 | 0.2162 % |
| 4051 | 16.85 | 135 | 2.8 | 0.07820 | 0.1955 % |
| 5400 | 12.68 | 180 | 2.8 | 0.07917 | 0.1979 % |
66:
| /mm | /° | /mm | (+200 mm) | (+200 mm)/% | |
|---|---|---|---|---|---|
| 1212 | 52.67 | 80 | 2.8 | 0.28600 | 0.3611 % |
| 1818 | 36.53 | 120 | 4.0 | 0.21012 | 0.2653 % |
| 2273 | 29.58 | 150 | 4.0 | 0.21428 | 0.2706 % |
| 2728 | 24.81 | 180 | 4.0 | 0.21714 | 0.2742 % |
Z(∞), das Bokehmaß
Jetzt noch schnell , d.h. für :
Diese Zahl gibt den Durchmesser eines Zerstreuungskreises eines weit entfernten Lichtpunkts hinter dem Objekt an, also z.B. Lichtkreise im Blätterdach, die klassischen Bokehbeipiele.